Shimeng Liu
In this study, I read behind the text of Alberta’s K–9 mathematics program of studies (Alberta Educa-tion 2007) by scrutinizing the metaphors it uses or implies in conceptualizing images of knowledge, learning and teaching.
Understanding metaphors and related associations embedded in curriculum sheds light on how concepts of mathematics learning and teaching are constructed. Metaphor fundamentally structures human conceptual systems and decisively affects our perceptions, thoughts and actions (Fauconnier and Turner 2008; Lakoff and Johnson 1980).
In the late 1990s, Sfard (1998) outlined two pre-dominant metaphors in learning mathematics—learning as acquisition and learning as participation—and their implications for educational practice. Since then, the realm of educational research has witnessed a more dynamic conglomeration of figurative associations acting to expand the interpretations of what knowledge, learning and teaching are. In addition to learning as acquisition and learning as participation, the metaphors of learning as construing and learning as viability-maintaining, along with their supportive ideas, are formulating into the grander networks of education paradigms. The four paradigms are standardized education, authentic education, democratic citizenship education and systemic sustainability education (Davis 2018).
The Discourses on Learning in Education website maps the pre-dominant discourses
around these education paradigms and the associated metaphors commonly applied to the school setting.1 It draws from a wide range of sources, including scholarly publications, research reports and other professional resources. My findings are drawn from metaphors and definitions documented on this web-site. Revealing fragments of the underlying education paradigms, metaphors in a curriculum framework disclose the beliefs that go into daily pedagogical practices without profound reflection.
Returning to Alberta’s K–9 mathematics program of studies (Alberta Education 2007), I will first examine the preamble and then move to the conceptual frame-work for K–9 mathematics and student outcomes. A careful textual analysis, with a focus on the early years (K–4), reveals a multi-metaphorical structure rooted in the discursive and conceptual system. This indicates the palimpsest-like composition of the curriculum. A palimpsest, which is a widely used trope in studying
cultural discourses, is a parchment on which layered traces from past writing can be seen, and the term has come to refer to the idea of superimposed temporalities (Stam 1997).
The program of studies presents its palimpsestic discursive multiplicity in using metaphors to convey the struggle between correspondence and coherence discourses in conceptualizing mathematics learning and teaching. More specifically, assumptions from mentalism permeate the text, ideas of constructivism are foregrounded in depicting learning and learner, and awareness of complexity discourses is emerging but not confirmed.
Correspondence and Coherence Discourses
Table 1 is an overview of the metaphors for knowledge, knowing, learner, learning and teaching used in the preamble to Alberta’s K–9 mathematics pro-gram of studies. It also lists the learning theories associated with those located metaphors and the learning discourses (correspondence or coherence) that the learning theories belong to.
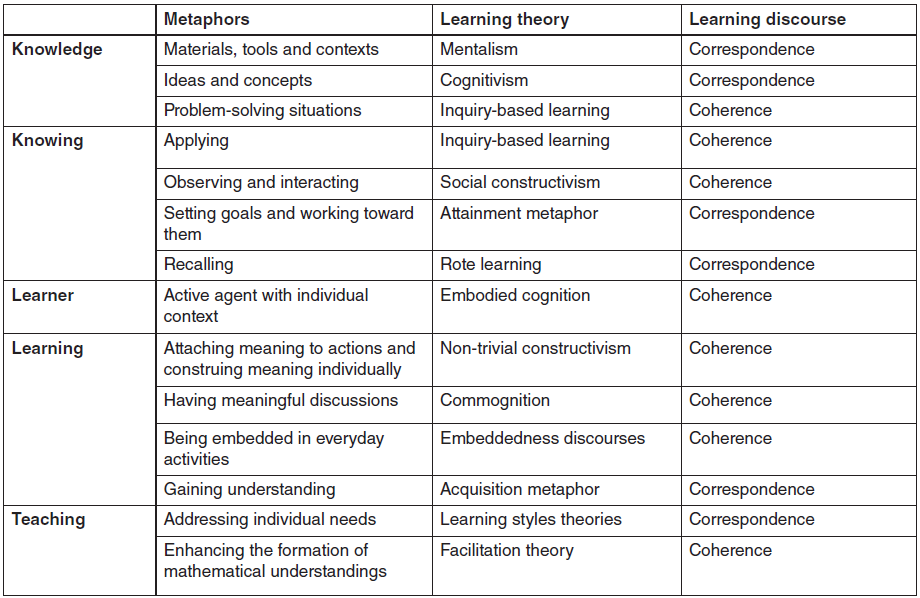
The correspondence discourses are a set of theories about learning that assume the separation of mind and body and that perceive learning as setting up a correspondence between the outer, objective world and the learner’s inner, subjective world.2 For ex-ample, cognitivism—which is nested in the correspondence discourses and originates from the metaphor of the brain as a digital computer (Searle 1990)—understands knowledge as information and learning as acquiring and retrieving ideas or concepts from the outside. A more commonly known example of a correspondence discourse is rote learning, a learning theory that emphasizes knowing as recalling and learning as storing memorized information.
In contrast, the coherence discourses do not perceive learning as being generated from the correspondences between the external and the internal. Rather, they understand knowledge as an interconnected system and the learner as “an evolving coherence” that continuously adapts to the web of meaning and interpretations through experiential being. For in-stance, inquiry-based learning focuses on learning as problem solving in authentic contexts and knowing as the learner’s intellectual and physical participation in generating knowledge. Likewise, embodied cognition views the learner as a social-cultural-situated bodied agent and learning as being initiated with bodily movements and perceptions.
In the context of the program of studies, the object-related metaphors align with correspondence dis-courses, and the ecological-based metaphors respond to coherence discourses.
The program of studies depicts knowledge of mathematics as materials, ideas and situations. It states that working with “materials, tools and con-texts” (Alberta Education 2007, 1) helps students construct meaning about mathematics. This aligns with the mentalism learning theory, which posits that knowledge is constituted by facts of the objective world and that subjective interpretation needs to be created by internalizing those external truths. For example, the program of studies states that through communication, students build “links among concrete, pictorial and symbolic representations of mathematical concepts” (p 1).
Existing as the objectified reality, mathematics knowledge can be gleaned from its various forms (materials, visuals and symbols), but the contents are ideas and concepts. Cognitivism also assumes that knowledge exists as information but uses the metaphor of the brain processing knowledge like a computer.
In the program of studies, reasoning and thinking in “problem-solving situations” are the foundation for students “to develop personal strategies and be-come mathematically literate” (p 1). Thus, mathematics knowledge can also be seen as inquiry. In inquiry-based learning, students become an indispensable part of knowledge production by exploring problems and applying their individual epistemological resources.
The idea of knowing as applying is consistent with the idea that mathematics knowledge is produced in situations of inquiry, indicating the context-dependent nature of understanding mathematics.
As noted in the program of studies, the sense-making of young children is stimulated by their observation and interaction “embedded in everyday activities” (p 2), both in and out of school. This stance extends mathematics knowledge from classroom-based situated inquiry to the broader social constructs. In social constructivism, knowing means to observe and interact with others as social practice.
However, as indicated in the program of studies, knowing also necessitates that students “set achievable goals and assess themselves as they work toward these goals” (p 2). As one of the most powerful folk theories in formal education, the attainment metaphor sees mathematics as a specific field wherein students learn by following a path and reaching milestones.
Occasionally, the program of studies indicates that knowing also involves recalling concepts (p 10), which is rote learning. This goes back to the mentalism that mathematics knowledge is context-free ex-ternal truths and that knowing requires memorizing and retaining information.
As the program of studies emphasizes, learners are active agents with individual contexts, bringing their own prior knowledge, experiences and backgrounds to the learning community (p 1). This implies an as-sociation with embodied cognition, which assumes that learning starts with physical movements and perceptions and then is refined and blended into higher-order concepts within one’s sociocultural context.
However, metaphors for learning go beyond embodied cognition to embrace a group of analogues with conflicting connotations.
First, the program of studies suggests that learning could be seen as attaching meaning to actions and constructing (or construing) the meaning of mathematics individually (p 1). Learning as construing implies the perspective of non-trivial constructivism because of its focus on the individuality of meaning production derived from experiences.
Second, learning could be having meaningful discussions about mathematics (p 1). Learning as interaction through communication, or commognition, “foregrounds the role of verbal language” in generating knowledge.
Third, learning mathematics could involve ordinary activities, such as playing or baking (p 2). Seeing learning as embedded in everyday activities refuses the division between self and other, body and mind, and individual and collective, suggesting an affinity with embeddedness discourses, which “understand[s] social and cultural collectives as dynamic, learning phenomena.”
Last, learning is to “gain understanding” (p 3) and to attain specific skills and knowledge (p 9), which signifies acquisition metaphor.
As with the other four constructs, teaching is presented in the program of studies with polarized metaphors and implied meanings.
As to the role of the teacher, the program of studies states that “through the use of manipulatives and a variety of pedagogical approaches, teachers can ad-dress the diverse learning styles, cultural backgrounds and developmental stages of students” (p 1), while promoting robust mathematical understanding. Learning styles theories see the learner as “an information processor,” with individual personal characteristics and preferences, and teaching thus means arranging information according to the peculiarities of each learner and making the inputting of that information smoother.
Another metaphor used in the program of stud-ies—teaching as enhancing the formation of mathematical understandings (p 1)—speaks to facilitation theory, in which there is a “positive learner–teacher relationship” and teaching is facilitating mathematical interpretation in the learner.
Thus, the program of studies interweaves learning styles theories (from the correspondence discourses) with facilitation theory (from the coherence dis-courses), creating paradigmatic tensions.
Mentalism, Constructivism and Complexity Perspectives
I also investigated the stated learning outcomes and beliefs about mathematics in the program of studies to determine whether they are in accordance with assertions made in the preamble.
The concept of performance outcomes itself is an inference made on the basis of standardized education, which was conceived as the foundation for industrial societies by taking knowledge as a standardizable object and the learner as measurable worker (Davis 2018, 188). Hence, the acquisition metaphor is intrinsic to the specific outcomes in the program of studies, which serve to “identity the specific skills, understanding and knowledge that students are re-quired to attain by the end of a given grade” (Alberta Education 2007, 9).
For instance, a Grade 1 student is expected to “estimate quantities to 20 by using referents” (p 13), in order to meet the standard of number sense development at this stage. This reveals a limited con-sideration of the “individual interests, abilities and needs” and “varying knowledge, life experiences and backgrounds” (p 1) mentioned in the preamble.
Nevertheless, the learning outcomes are not entirely confined within the perceptions of mentalism. While specifying outcomes, the program of studies does underscore the importance of daily activities in fostering mathematics understanding. This indicates agreement with non-trivial constructivism in the belief that knowledge is the “sum of already-established construals/constructs” and the learner is “a meaning-maker” who derives meaning from individual experience.
For instance, the number strand in the program of studies implicitly integrates Lakoff and Núñez’s (2000, 53) four “grounding metaphors” as strategies to develop higher number sense by correlating the innate capabilities of subitizing and counting with everyday activities. For example, the ability to “demonstrate an understanding of counting by . . . using parts or equal groups to count sets” (Alberta Education 2007, 13) involves the metaphor of “arithmetic as object collection” (Lakoff and Núñez 2000, 54).
“Demonstrat[ing] an understanding of fractions by . . . explaining that a fraction represents a part of a whole” (Alberta Education 2007, 21) suggests the metaphor of “arithmetic as object construction” (Lakoff and Núñez 2000, 65). Moreover, the “measuring stick metaphor” (p 68) and the “motion along a path” (p 71) metaphor could also be identified among the specific out-comes. In sum, knowledge of arithmetic as count, size, distance and position is not external truth to be transferred into the learner’s mind but, rather, the interpretations produced and refined by inter-connections of the learner’s intuitive understanding of numerosity with the experience of using objects.
Since mathematics is framed by “our bodies, our brains, and our everyday functioning in the world” (Lakoff and Núñez 2000, 5), the program of studies points out the mathematical processes of significance in achieving the outcomes: communication (C), connections (CN), mental mathematics and estima-tion (ME), problem solving (PS), reasoning (R), technology (T), and visualization (V) (Alberta Education 2007, 4).
Table 2 shows that in the program of studies the most frequently mentioned mathematical processes for each grade are connections in kindergarten; visualization in Grade 1; and communication in Grades 2, 3 and 4. Taking all the grades together, the top three processes are communication, connections and visualization.
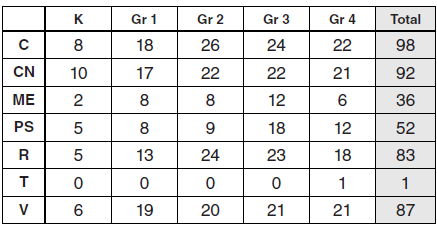
Communication refers to various modes of expression students can use to help them “make connections among concrete, pictorial, symbolic, oral, written and mental representations of mathematical ideas” (Alberta Education 2007, 5), and connections refers to “contextualization and making connections to the experiences of learners” (p 5), to each other and to the world beyond the classroom, for the sake of integrating mathematics into micro- and macro-coherence. Visualization refers to visual images, visual reasoning and spatial perception in making sense of number, geometric shapes and measurement (p 6). All three processes are interrelated and nested within each other. They represent the necessary steps before reaching “formalising understanding” (Pirie and Kieren 1994, 39) in mathematics development, in which the learner is able to move beyond using concrete objects in certain contexts into working with symbolic representations in diverse contexts.
The incongruity appears when communication, connections and visualization are not identified as pedagogical focuses in the conceptual framework for mathematics. Instead, the program of studies deems problem solving to be the mathematical process that is “the focus of mathematics at all grade levels” (Alberta Education 2007, 6), because it asks students to apply their prior knowledge to new contexts and “empowers students to explore alternatives and develops confident, cognitive mathematical risk takers” (p 6). Underlying this statement is the idea that mathematics knowledge represents a range of possibilities and that learning means expanding and transcending the given possibilities. Going back to Discourses on Learning in Education, this alludes to eco-complexity discourses, which is a subcategory of the coherence discourses that relies on ecological metaphors in perceiving learning as an evolving ecosystem of complexity.
A complex phenomenon has two characteristics: it is adaptive because it evolves its own structure, and it is emergent because of the co-evolving interactions of individual agents and the ensemble (Davis and Simmt 2003). The emergence of new knowledge and creativity goes hand in hand with transcendental moments in the collective of bumping ideas and bodies. For example, in a Grade 7 class learning multiplication, stimulating opportunities for mathematical engagement arise after intentional efforts have been invested in creating an adaptive and self-organizing collective of learning, rather than just a collection of individuals (Davis and Simmt 2003). Shifting dichotomies of person and nature, material and transcendent, and one and many into nested constructs, the complex system of learning does not view the learner as a discrete agent in their own existence but, rather, as an agent in the intersectionality of bodily, social, cultural and biological subsystems. This per-spective synthesizes the constructivist and sociocultural perspectives on mathematics development, be-cause of its emphasis on the inseparability between individual-in-construing and individual-in-social-action (Cobb 1994).
If we can say that the curricular focus on problem solving gestures toward the complexity perspective of mathematics education, then the implied text of the learning outcomes in the program of studies is calling for the return of constructivism, in which learning is individual doing and thinking.
Conclusion
In this study, I have striven to understand the metaphors attached to knowledge, knowing, learner, learning and teaching in Alberta’s K–9 mathematics pro-gram of studies. The findings reveal that underlying the curriculum is a pervasive wrestling between the correspondence and coherence discourses of learning, with a particularly strong voice from mentalism, a growing recognition of constructivism and an emerging awareness of complexity discourses.
Notes
- “Map,” Discourses on Learning in Education website, B Davis and K Francis, https://learningdiscourses.com /learning-discourses/ (accessed October 13, 2021).
- Information on this term and subsequent italicized terms comes from the alphabetical index of the Discourses on Learn-ing in Education website at https://learningdiscourses.com/alphabetical-index/ (accessed October 13, 2021).
References
Shimeng Liu completed a master of arts degree in learning sciences at the University of Calgary in 2020. Her thesis aimed to redefine mathematics learning for racialized immigrant, refugee and English-language learners in the early years. She also has a PhD in cultural studies from the College of Foreign Languages and Cultures of Sichuan University. After immigrating to Canada with her family, she taught mathematics and Mandarin to immigrant students. She currently works as a research coordinator and assistant for a project on science, technology, engi-neering and mathematics (STEM) learning.
Alberta Education. 2007. Mathematics Kindergarten to Grade 9 Program of Studies. Edmonton, Alta: Alberta Education. Also available at https://education.alberta.ca/media/3115252/2016_k_to_9_math_pos.pdf (accessed October 13, 2021).
Cobb, P. 1994. “Where Is the Mind? Constructivist and Sociocultural Perspectives on Mathematical Development.” Educational Researcher 23, no 7 (October): 13–20.
Davis, B. 2018. “On the Many Metaphors of Learning . . . and Their Associated Educational Frames.” Journal of Curriculum Studies 50, no 2: 182–203.
Davis, B, and E Simmt. 2003. “Understanding Learning Systems: Mathematics Education and Complexity Science.” Journal for Research in Mathematics Education 34, no 2 (March): 137–67.
Fauconnier, G, and M Turner. 2008. “Rethinking Metaphor.” In The Cambridge Handbook of Metaphor and Thought, ed R W Gibbs, 53–66. Cambridge: Cambridge University Press. Lakoff, G, and M Johnson. 1980. Metaphors We Live By. Chicago: University of Chicago Press.
Lakoff, G, and R Núñez. 2000. Where Mathematics Comes From: How the Embodied Mind Brings Mathematics into Being. New York: Basic Books.
Pirie, S E B, and T E Kieren. 1994. “Beyond Metaphor: Formalising in Mathematical Understanding Within Constructivist Environments.” For the Learning of Mathematics 14, no 1 (February): 39–43. Also available at https://flm-journal.org/Ar ticles/83AE5FE212FCAC7DB193917FADF90.pdf (accessed October 13, 2021).
Searle, J R. 1990. “Is the Brain a Digital Computer?” Proceedings and Addresses of the American Philosophical Association 64, no 3 (November): 21–37.
Sfard, A. 1998. “On Two Metaphors for Learning and the Dangers of Choosing Just One.” Educational Researcher 27, no 2 (March): 4–13.
Stam, R. 1997. “From Hybridity to the Aesthetics of Garbage.” Social Identities 3, no 2: 275–90.






