Lynn McGarvey
In “Producing Equivalent Fractions ‘Additively’: The Case of the 1/2,” Jérôme Proulx shares an experience familiar to teachers of mathematics, from kindergarten to postsecondary.
In this experience, we are engaged in mathematical discussion with students, and they generate a new idea, solve a problem in a novel way or ask a question we had not considered before. Even though we tell our students that mathematics is about problem solving, curiosity and persistence, we may experience a moment of panic if we do not immediately understand their question or know the answer.
How we respond in those moments says a lot about our own mathematical disposition. Do we gloss over the problem, downplay its importance or simply ignore it? Or are we willing to acknowledge that we don’t know and then try to figure it out with the class, in the staff room at lunch or on our own? In his article, Proulx demonstrates all of the positive dispositions we want to see in students and teachers, including inquisitive-ness, perseverance, confidence and sensemaking.
Reinterpreting the Problem: Consecutive Equivalent Fractions
The problem posed in Proulx’s article wasn’t one I had considered before. But mathematics isn’t something you can read. It is something you have to do. So even though I read through the draft of the article, my margin notes showed that I, too, needed to work through the mathematics—usually in a different way from Proulx.
The general problem, as I interpreted it, was that of consecutive equivalent fractions, in which the numerators of two equivalent fractions had a difference of one (for example, 4/8 and 5/10). Although Proulx focuses on producing equivalent fractions “additively,” I continued to forefront the notion that equivalent fractions would always have a multiplicative relationship.
Proulx presents the following representation of adding 1 to the numerator and 2 to the denominator to get another equivalent fraction in the form of one-half:
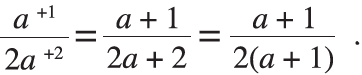
While I understood the equation presented, I re-wrote it in the margin as
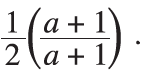
This revision to the equation provided a new insight for me. We typically emphasize the multiplicative relationship between equivalent fractions and use it to generate new fractions. For example, if we examined the relationship between 4/8 and 5/10, we would usually show it as follows:
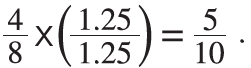
This approach emphasizes the multiplicative relation-ship, but the fact that the numerators differ by 1 simply gets lost.
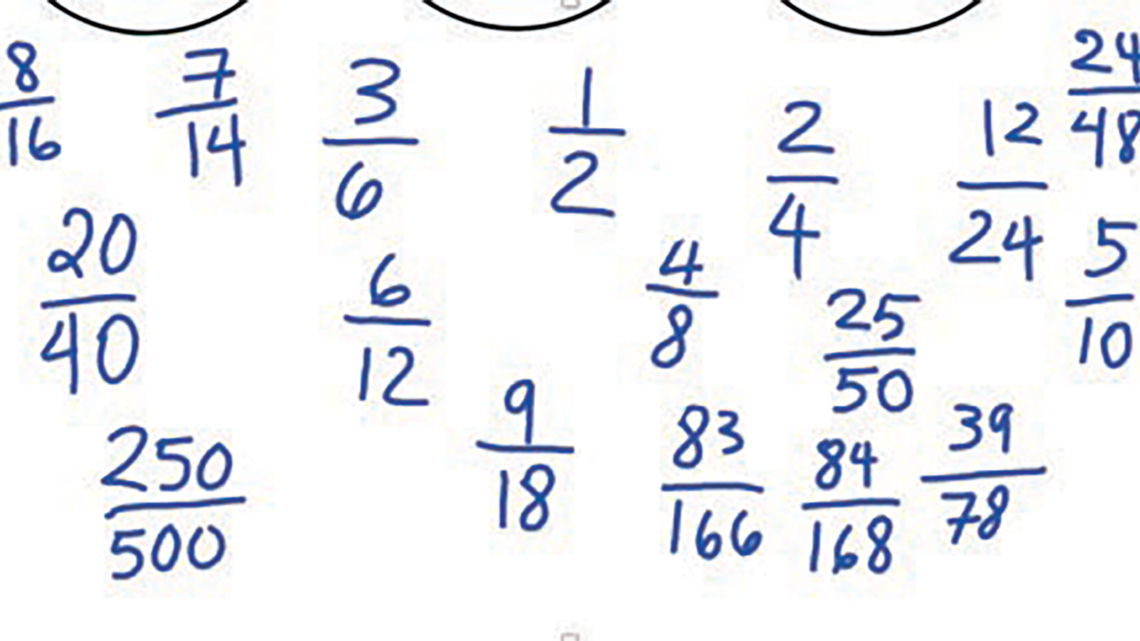
I thought more carefully about the fact that all fractions that are equivalent to one-half are derived from the unit fraction of 1/2. Figure 1 shows my margin notes.
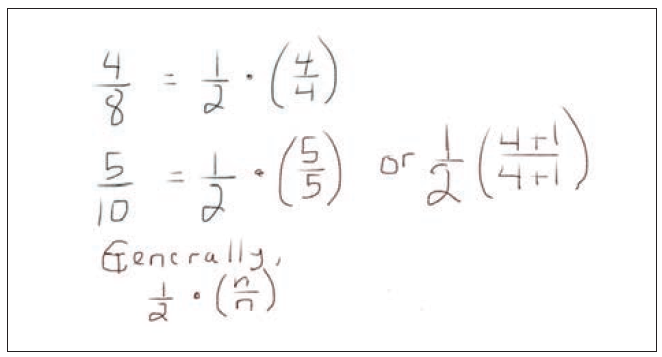
We can generate “consecutive” equivalent fractions by starting with the unit fraction, using
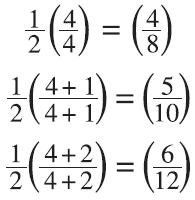
So equivalent fractions of one-half, one-third or any unit fraction can be multiplied by any whole—a/a or (a + 1)/(a + 1)—to generate or analyze consecutive equivalent fractions.
Visualizing Consecutive Equivalent Fractions
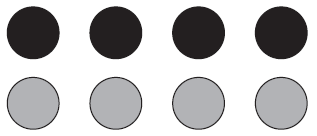
The other challenge Proulx presents is how to visualize these consecutive equivalent fractions, particularly since our methods usually involve partitioning an area or measurement model into smaller but equivalent parts. We could, however, employ a sets model to illustrate the “plus 1” nature of equivalent fractions.
For example, in Figure 2, 4/8 of the set is black.
We can use the equation
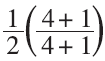
to illustrate “plus 1” to the numerator and denominator to generate the equivalent fraction, 5/10, as shown in Figure 3.

In both cases, we can say that 4/8 and 5/10 are generated from the unit fraction 1/2 (Figure 4), where both numerator and denominator are multiplied by the same whole—either 4/4 or (4 + 1)/(4 + 1).

Closing Remarks
I recognize that in making sense of the problem posed by Proulx, I have reinterpreted it and examined it from a different perspective. Such is the beauty of mathematics. I expect that every article with a mathematical curiosity can be examined and explained from different perspectives.
It is interesting that even as I write this response, I wonder how it will be critiqued. That underlying feeling of uncertainty when presented with a novel problem doesn’t necessarily dissipate after you have worked through a problem on your own. However, as teachers, we need to be curious and courageous and to put our mathematical thinking out there, so that others can engage in the problem and offer their own ideas and interpretations.
Lynn McGarvey, PhD, is a mathematics education professor in the Faculty of Education, University of Alberta. Her research focuses on the mathematical understanding of children, youth, and preservice and in-service teachers in the context of spatial and algebraic reasoning. She currently serves as vice-dean and associate dean (academic) of the faculty.