Sally Rudakoff and Steven Khan
Teachers are still struggling with understanding computational thinking vs. coding and how it relates to their curriculum. As well, some see this as an “add-on” that they don’t have time for. I hope if we emphasize computational thinking skills in [the] elementary [grades that] students will begin to develop skills and concepts that will follow them as they advance through our school system.
Sally
Proto-Computational Thinking (PCT) might be a more realistic and achievable systemic goal for naming what we do at the earliest grade levels in a way that is intellectually honest and respectful of the multiple responsibilities around learner competencies that teachers are already charged with (read responsible or accountable for) developing.
Steven1
We, the authors of this article, have responsibilities related to supporting teachers’ growth at various stages in their careers. In both of our contexts—pre-service teacher education and school district numeracy and technology support—we have noticed K–6 teachers’ interest in and struggles with the relationships between computational thinking, coding and the existing curriculum. At the same time, we are attuned to concerns in the literature about levels of enactment (Namukasa 2018) and the challenges posed by the multiple origins, definitions and frameworks for the practice and study of computational thinking in multiple environments (Khan et al 2017).
We see our discussion here as propaedeutic—a preliminary excursion and exploration that invites
readers to attend to the possibilities for mathematics and computational thinking in children’s life-worlds. Computational thinking can be defined as “solving problems, designing systems, and understanding human behavior, by drawing on the concepts fundamental to computer science” (Wing 2006, 33). In a more recent review, Shute, Sun and Asbell-Clarke (2017, 142) define it as “the conceptual foundation required to solve problems effectively and efficiently . . . with solutions that are reusable in different contexts.” Indeed, what separates computational thinking from other forms of mathematical problem solving is the ability to extract or abstract the answer into other domains and apply the solution to other cases. Khan et al (2017, 5) adopt a sociocultural approach to computational thinking, taking it as “an enculturated set of human practices to see, hear, encounter, and ultimately read and write the world, in a Freirian sense, in particular ways that are valued/rewarded in specific computational cultures.” Ultimately, computational thinking is a literacy practice (Bers 2017) that is essential for understanding and participating meaningfully in the transformations of all areas of life in the 21st century (Kafai and Burke 2014).
Figure 1 shows how we conceptualize the place and importance of computational thinking from a complex systems (or transdisciplinary) perspective. In our framework, foundational computational experiences are necessary (but not sufficient) for developing computational identities (including disposition), which contributes to developing computational thinking in diverse computational communities. Such communities require members
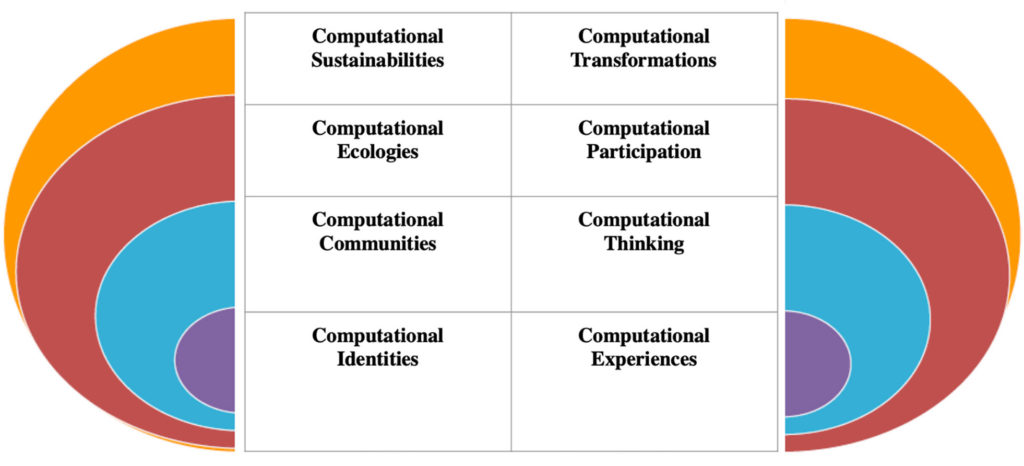
to participate meaningfully in diverse ways (for example, as coders, legislators or critical consumers) and give rise to webs of connected computational communities or computational ecologies. These computational ecologies contribute to the ongoing transformation of social, political, economic and ecological life-worlds and necessitate thinking in terms of their ethics and sustainability with regard to human and planetary flourishing. Our work here and that of others in early learning, such as Kotsopoulos et al (2019), is situated at the base of these nested systems—a consideration of an early experience of computational thinking and its potential for contributing to the development of some aspects of a computational identity (in particular, those aspects related to computational disposition).
Here, we think through how one might use Archelino—a commercially available (but easily generalizable) wooden logic puzzle game—to develop one aspect of computational thinking: the ability to see problems as decomposable and recomposable for learners aged four to eight years old (pre-kindergarten to Grade 3) and preservice teachers. We suggest ways that the critical aspect (Marton 2014) of decomposing and recomposing problems, while working toward a clearly defined goal, is a necessary component of computational thinking that can be developed through attending to the design of the puzzles offered by commercial logic games. We also draw attention to how the game might contribute to the development of a healthy computational disposition (Pérez 2018).
The activity we describe can be used with a whole class, with small groups or partners (station work), or at home (with parental support). Archelino presents opportunities for problem solving (especially logical reasoning) at various levels of difficulty, allows for differentiation with students who are in the early stages of developing understanding of the concept, and highlights the importance of sequencing/ordering (algorithmic thinking) and decomposition. It also affords opportunities for developing understanding of positional language related to spatial reasoning—a common learning outcome across Canadian and international curricula.
To be clear, we are not arguing that this should be the only experience learners have with sequencing/ordering and decomposition, or the only place to develop a computational disposition. As Resnick (2016) writes,
For a technology to be effective, . . . it should provide easy ways for novices to get started (low floor) but also ways for them to work on increasingly sophisticated projects over time (high ceiling). . . .
. . . For a more complete picture, we need to add an extra dimension: wide walls. It’s not enough to provide a single path from low floor to high ceiling; we need to provide wide walls so that kids can explore multiple pathways from floor to ceiling.
We believe that Archelino, along with focused, pedagogically informed teacher- or parent-led questioning or discussion, provides excellent low-floor entry points for educators and students to begin discussing computational thinking concepts, with good potential for high ceilings and wide walls. We will not here discuss using this activity as a form of assessment, though the formative assessment aspects are evident to us as teachers, especially in student–teacher direct engagement and questioning.
We hope that teachers and other readers see how whole-class or partner activities like this can contribute to developing critical foundational aspects of both mathematical thinking and computational thinking simultaneously in young learners, as well as a productive disposition toward learning. We also hope readers will seek out and share additional opportunities with each other and the wider community, and that they will continue to develop the activity in order to draw attention to other aspects of value and to opportunities for learning that we have not yet considered.
About Archelino
Archelino is a commercial logic puzzle game created by Inon Kohn and distributed by the German game company HUCH! The game is recommended for ages four and up; it requires one or more players, and the typical playing time is approximately 10 minutes.
The game set consists of one grooved wooden ark; seven wooden figures (Noah and six animals), each about two inches tall; a puzzle book containing 60 puzzles in the categories of starter, advanced, expert and master; and one multilingual instruction booklet (see Figure 2). The game is based on the story of Noah’s ark, with the premise that each animal wants to sit next to or converse with another specific animal. The essence of the game, however, can be recreated with other story scenarios not tied to this particular narrative.
Archelino allows players to solve puzzles that present a visual description of how the animals should be ordered from left to right (first, second and so on), how they should be oriented (facing left or right), and whether they want to converse (facing each other). The goal is to use the visual clues to solve the puzzle by correctly ordering, orienting and sequencing the animals on the ark. The instruction booklet and box art explicitly state that learning to think strategically is the main affordance of engaging with the puzzle.
Archelino retails for approximately C$29 on Amazon.ca and C$25 on FoxMind (www.foxmind .com). Considering the wider social content and

taking a critical view of our work, we acknowledge that, as with many durable wooden resources for early learners (for example, traditional Montessori and Waldorf materials), price can be an access barrier for individuals, schools and districts. At the same time, the organizations we work for have developed and maintain libraries that lend materials such as games, puzzles and technological devices, and the public library system enables teachers and parents to access similar resources through requests and delivery to community branches. Also, at thrift stores we often find wooden animal toys that could be used in place of the Archelino materials.
In the next section, we elaborate on the specific affordances we see for developing a computational thinking skill—decomposition and recomposition—in the context of Archelino.
Choosing Archelino
We would like to say that we did an exhaustive exploration of a number of commercial games and picked the one best suited to our purpose, or that we reviewed lists of award-winning toys. However, the truth is more mundane—and, we believe, more typical of how games like Archelino get considered and incorporated into teaching and learning at home, in school settings, and in extracurricular or cocurricular groups.
A departmental colleague of Steven’s, who does research on commercial games and who is also a parent, suggested the game to him for use with his three-and-a-half-year-old daughter. This was around the same time we were having conversations about the difficulties teachers have in thinking about com-putational thinking in elementary schools. Alberta’s current curriculum does not explicitly name anything as computational thinking, but the draft K–4 revised mathematics curriculum—which we both independently reviewed in our respective professional capacities—foregrounds aspects related to algorithmic thinking.2 We were interested in finding ways to support preservice and inservice teachers as they try to integrate and incorporate computational thinking ideas in that context. We saw an opportunity for learning, and we took it.
We had another moment of insight when we were working with Archelino while thinking about the learning of elementary mathematics alongside computational thinking. We had several moments of recognition in making connections by seeing—and naming—the familiar (decomposition) in the unfamiliar (a puzzle game context). We feel that it is also important to draw attention to such occasions that provide opportunities for building learners’ capacity for transfer (Salomon and Perkins 1989), especially through noticing (Lobato, Rhodehamel and Hohensee 2012), from singular embedded learning experiences to more general applied learning in different contexts across time.
Our modest hope is that by encouraging teachers (and parents) to find the familiar in unfamiliar places, by choosing to bring opportunities for distal connections across multiple types of mathematical texts, and by guiding students to make those connections explicit (notice, name and nurture) through meaningful questioning or discussion, we can increase the probability that learners will see the relevance structure (Marton 2014) and potential of learning in general in multiple contexts. We note that educating for far transfer of learning remains an elusive goal in many areas but especially in the area of computational thinking, where the evidence for such claims is weak (Denning 2017). With a pedagogical program of selectively experimenting in deliberately combinatorial ways to prevent ideas from becoming inert (Whitehead 1967), we see increased probability of far transfer and meaningful, joyful learning.
When we were revising this article, one reviewer asked if we could offer examples of what far transfer might look like in the context of the particular learnings from this game and how one might look for far transfer. We acknowledge the value of this request and state that part of the difficulty of recognizing far transfer is that it often becomes evident long after the initial foundational experiences and cannot be explicitly drawn upon as easily as a causal phenomenon. Another difficulty with far transfer is that in real life multiple confounds occur as experiences leach into each other over time. In the case of the affordance of discerning decomposition/recomposition in this game, one might see near transfer in the short term of decomposing problems in other areas not explicitly mathematical or computational (for example, sports, cooking, science or the fine arts). Making a strong claim about far transfer is not easy, and it is precisely the overblown claims in much of the literature related to computational thinking in education that Denning (2017) explicitly critiques. Our position is to proceed cautiously, with modest claims about what might be discerned in this game while acknowledging that learning involves multiple opportunities for recursive elaboration over time and contexts.
Discernment in Variation Theory
Discernment—or the coming into conscious awareness of an object, relation, concept or phenomenon of which one was not previously consciously aware—is a focus of the variation theory of learning (Marton 2014). The aspects of the object of learning (what one is trying to learn or to have a learner notice and become aware of) are referred to as the critical aspects. So, for example, one could say that Hoyles and Noss’s (2015) framework for computational thinking has four critical aspects—pattern recognition, decomposition, abstraction and algorithm design—that are to be discerned and developed by the learner, with the help of the teacher and the learning materials.
Low-floor puzzle games (such as Archelino) offer an opportunity for what Trninic (2018, 150) describes as “explorative practice”: “a pedagogical approach with a high degree of guidance but a minimal degree of explaining.” Trninic draws on Freudenthal’s (1971) suggestion that learning mathematics (specifically, geometry) should be like learning to swim. In swimming lessons, a qualified teacher helps the learner come to sensory-motor and conscious awareness without initially offering explanations. This keeps the learner’s limited attentional (cognitive-emotional) resources focused on a small set of critical aspects that are important in that moment.
Discerning Decomposition in Archelino
The ability to decompose a problem into smaller components is seen as an important aspect of both computational thinking and mathematical problem solving (Hoyles and Noss 2015; Polya 2014). It is also a core component of other computational thinking frameworks, such as Computing at School’s concepts of computational thinking (Csizmadia et al 2015, 8) and the International Society for Technology in Education (ISTE) Standards for Students (under Computational Thinker).3
Figures 3–7 show several of the Archelino puzzle clue cards and the possible discernments. Players are presented with these cards one at a time, and are instructed to place the animals in the same sequence as depicted on the card or to determine the sequence of all the animals in the ark. We have arranged these clue cards in a sequence to show some of the discernments they make possible.
After exploring the puzzles, we explicitly labelled the concept we saw with the sequencing of puzzle clues as decomposition—that is, breaking down the general problem of placing the animals in the correct order (sequence) into a set of two or more discrete, non-overlapping puzzles. We also noticed that none of the clues contained redundant information (such as placing the same animal in its correct position in more than one clue).
We observed that when learners attempted to do puzzle 4 (see Figure 4), it was critical for them to first understand what the image represented. A young child’s interpretation and the questions asked by several preservice teachers who played the game suggest that they saw the two images as discrete situations—asking, “Do I need two arks?”—and not as a decomposed clue to the general goal of placing the animals in the ark in the right order and orientation (facing left or right). This, we believe, offers the opportunity to draw learners’ awareness to the representation in the puzzle clues as a decomposition of the final goal (placing all the animals in the correct order). Puzzles 7 (Figure 4) and 11 (Figure 5) continue this elaborative explorative practice—first, with a puzzle that is decomposed in a continuous piecewise manner, and then with a puzzle in which the animals are unevenly distributed.
We recognize that naming this process decomposition was a result of priming ourselves beforehand by considering what aspects of computational thinking might be present in this game. We had an intuitive sense that the actions the game guides players to explore could be framed within the educational discourse of decomposition. Having thus recognized the naming as a function of priming, we note that decomposition in computational thinking (in this case, with Archelino) is an illustrative example of Polya’s (2014) more general heuristic regarding decomposing and recombining in problem solving, which involves analyzing a problem and breaking it into smaller, discrete problems, the sum total of which solves the original problem.
We also want to emphasize that while the sequence of puzzles in Archelino teaches the idea of decomposition, nowhere does the game explicitly name it as such, nor would we expect teachers (or parents) to do so without prompting or consideration of the particular affordances for learning. We also note that in developing explicit conscious awareness of this critical aspect of computational thinking, it is important for teachers to place a semiotic linguistic marker on the necessary aspect of the experience—that is, to label the puzzle image as “a decomposition into two parts,” “a decomposition into three parts” and so on. If teachers explore and name decomposition with students in an explicit teaching opportunity, students will, ideally, be able to make connections to the importance of decomposing in other situations.
In the next section, we discuss our approaches to and strategies for playing Archelino (including our differing strategies) and move into how teachers might use the game in the classroom in various formats.
Affordances for Developing Computational Thinking
Initially, we each played the game individually. Steven also played it with his three-and-a-half-year-old daughter. We then discussed how our strategies differed for some puzzles.
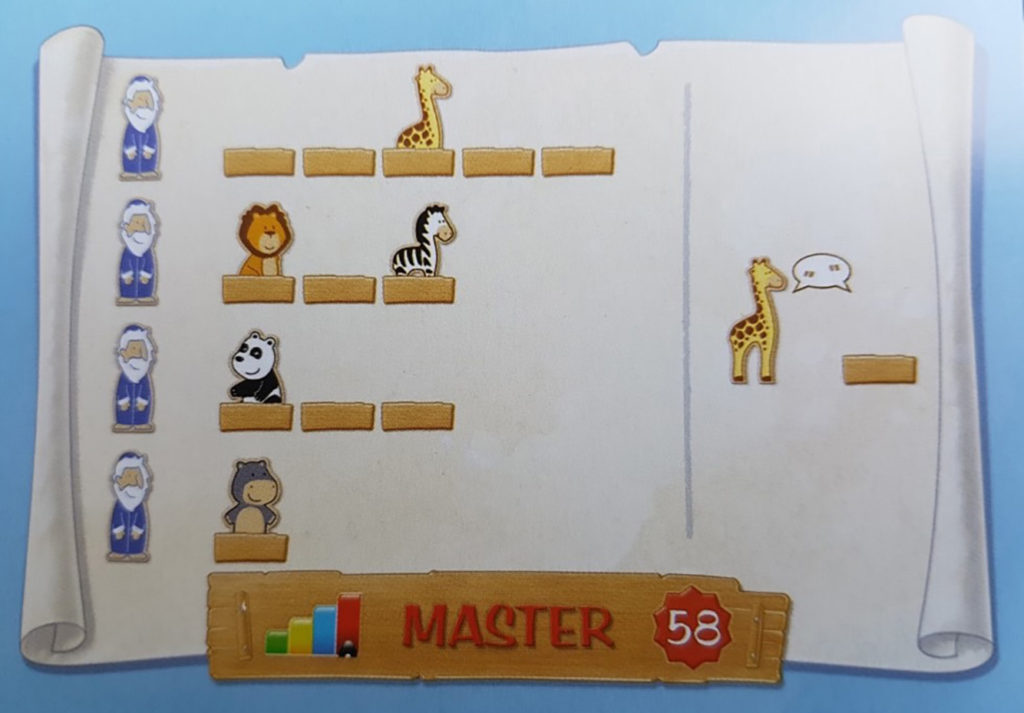
For example, in puzzle 9 (Figure 8), Sally’s strategy involved following each line of the visual instructions and enacting them sequentially: first, placing the giraffe and the kangaroo; then, placing the hippo and the lion; and, finally, placing the zebra and the panda. Steven’s strategy involved working across the three clues to place the animals serially, following the ordinal numbers: placing the giraffe and then the hippo, the zebra and the panda, the lion, and, finally, the kangaroo.

Sally’s Strategy
• The giraffe is in the first position, facing to the right.
• The kangaroo is in the last/sixth position, facing left.
• The hippo is next to the giraffe, facing the giraffe.
• The lion is next to the kangaroo, facing right.
• The zebra is to the right of the hippo, facing right.
• The panda is facing the zebra.
Steven’s Strategy
• The giraffe is in the first position, facing right.
• The hippo is in the second position, facing left.
• The zebra is in the third position, facing right.
• The panda is in the fourth position, facing left.
• The lion is in the fifth position, facing right.
• The kangaroo is in the sixth position, facing left.
As we talked about our different approaches, we came to appreciate not only that we approach puzzles differently but also that there is value in someone else’s approach. These are valid alternative strategies, and they both will lead to successfully solving the puzzle. In a classroom, a small group or a teacher interview setting, allowing students to see and make sense of alternative strategies is important. This increases both the personal example space of strategies of which students are aware and the potential for students’ flexible thinking when working on future puzzles.
Other ways of giving the instructions can draw attention to the structure of the visual clues in a mathematical way. For example, a preservice teacher in a workshop setting stated, “The animals are arranged in pairs facing each other; there is an AB repeating pattern.” With a similar puzzle, a preservice teacher noticed that “animals placed on odd-numbered spaces are facing left, and animals placed on even-numbered spaces are facing right.” The existence of a number of valid ways to approach the problem (depending on what is noticed and attended to) and the opportunity to bring in a variety of mathematical ideas are characteristic of a good low-floor task for elementary learners. Working one-on-one with students allows teachers to use deliberate questioning to further investigate their chosen strategies and the mathematical thinking behind their responses.
The observation that there are multiple ways to provide instructions that result in the same goal using different mathematical concepts is meaningful in the context of Rich et al (2017), who argue for an “offline-before-online heuristic” in learning computational thinking. They begin their sequencing trajectory with two fundamental ideas that relate to the Archelino puzzles. The first idea focuses on the importance of specificity when giving instructions, and the second explores the importance of the order of the instructions, as changing the order can lead to different results.
Adapting for a Partner Activity
When we were discussing our strategies, the idea emerged to play Archelino as a two-player game, with one player translating the visual clues into oral instructions and the other player building the sequence. This approach is related to our familiarity with barrier games in elementary education. Playing in this way, with the two players alternating roles, also allows for immediate feedback and a sort of debugging of instructions, as the translator can see immediately whether the builder has carried out the instructions correctly or whether steps are missing or unclear.
Displaying a poster with question prompts along-side the game would be beneficial for students when playing with a teacher or a partner. These questions could be used during the game or after solving the puzzle (as an opportunity for reflection). Questions could include the following:
• Why did you choose _________ as your first move?
• What did you first notice when looking at the visual clue?
• What strategy did you use to solve the puzzle?
• Did you notice a pattern when looking at the visual clue?
• How did you know to place the _________ in that spot?
• How did you know to place the _________ facing left?4
Demonstrating this type of questioning with parents and preservice teachers helps them to notice important aspects of the game play and to nurture students’ thinking, problem-solving and oral communication skills. We also note the increased challenge and cognitive demand involved in attempting to verbalize visual instructions and how this verbalization helped us attend differently and effortfully to critical aspects such as the orientation of the figures, their relative positions and the sequence in which we gave the instructions, especially with the more challenging puzzles.
Adapting for a Whole-Class Activity
Exploring the activity as a class before having students play Archelino as a two-player game has benefits. It enables students to build an understanding of the goals and purpose of the activity and prepares them for playing the game with a partner. Doing a whole-class activity also allows the teacher to provide students with the appropriate language to use when completing the activity and to offer suggestions for problem solving. Here is an example of how such an activity can be structured:
- To begin, invite six students to the front of the class to represent the six animal figures on the ark. You may want to use hats or coloured fabric to identify them, as they will be moving around.
- Tape an ark (a number line) to the floor so that students know where to stand. You can identify one student as Noah to stand at the front of the ark.
- Display a visual clue on the board, using a document camera or a slideshow projector.
- Give students quiet thinking time to explore how they would place the animals on the ark.
- When students are ready, select one student to give oral instructions to the students who are represent-ing the animals so that they appear on the ark exactly as they do in the visual clue.
- In addition to giving oral instructions, students can be responsible for moving the animals into the correct order on the ark.
- Invite students to use various strategies to place the animals on the ark, and take the time to explore their differing strategies.
- Once the animals are in the correct order on the ark, students can discuss their strategies and how they solved the visual clue.5
This approach resonates with Sung, Ahn and of moves on a number line and enacting the composition of moves in addition.
Abstracting to Other Games and Representations
The Archelino game was a convenient choice for us. However, other commercially available games could be used to explore the same ideas. The animal figures in the Archelino set could be replaced with more readily available and affordable items (such as connecting cubes, recycled plastic toys or tangram animals) (see Figure 9), though we do not underestimate the value of investing in high-quality wooden toy puzzles and manipulatives that will last for many years and classes. The most important aspect of the Archelino set is the puzzle cards, and parents and preservice and inservice teachers should spend time thinking about how the puzzles are sequenced if they plan to remix this game using different materials or scenarios.

In the next section, we discuss an affordance for developing computational thinking dispositions with Archelino.
Developing Computational Thinking Dispositions
Computational thinking disposition refers to “the willingness and opportunity to make use of [student] knowledge and ability” in the area of computationalthinking (Pérez 2018, 427). According to Pérez, students must develop computational thinking dispositions if they are to derive benefit from meaningful computational thinking learning opportunities presented in classrooms in mathematical contexts. In addition, if students can recognize computational thinking opportunities on their own, they will then be able to “recognize, respond to, and appropriately act” (p 428) on these opportunities.
Pérez’s framework for the three necessary dispositions for computational thinking—tolerance for ambiguity, persistence and collaboration—is relevant to the Archelino game and can also be used when working with students on developing their computational thinking dispositions. Next, we elaborate on these dispositions and how they can be developed with Archelino.
Tolerance for Ambiguity
Pérez (2018, 444) describes the first disposition—tolerance for ambiguity—as “a tendency to experience ambiguous situations or stimuli as enriching and engaging.”
As noted before, Archelino puzzle 4 (Figure 4) is an ambiguous visual stimulus for some learners and requires interpretation and teacher intervention to explain the connection between the puzzle clues and the task goal. This is an easily resolved ambiguity. When working in partners, for example, one learner must listen attentively and carefully to the oral instructions given by the partner and try to place the animals in the correct sequence and the correct orientation. Depending on the degree of specificity of the oral instructions (for example, the mathematical language used), in addition to various possible solution pathways, both learners may experience what we will call productive ambiguity (as an analogue to productive struggle). This requires them to find ways to reduce the ambiguity (for example, by asking clarifying questions) and move toward successfully completing the puzzle.
Teachers have a tendency to too quickly reduce such ambiguity for students in the same way that they sometimes too quickly reduce the cognitive demands of a task, which takes away learners’ experience of productively struggling with the mathematics—the work of learning. We see a need (and an opportunity through playing Archelino) to give students more opportunities to experience productive ambiguity and to work to resolve—communicatively, mathematically and computationally—ambiguous situations that are nonthreatening. This helps build their confidence and questioning skills for when they face challenging cognitive tasks involving decomposition.
Persistence
Persistence is a necessary and valued habit for learners of all ages. It is related to developing resilience in challenging contexts, such as problem solving and computational thinking (with or without coding).
In Archelino, students display task persistence as they work to successfully complete the puzzles. Pérez (2018) argues that the classroom environment and learning opportunities should encourage persistence among students in order to develop this disposition.
To develop persistence, students need challenging tasks at the appropriate cognitive level that offer positive reinforcement upon completion. They may need numerous attempts to complete some puzzles, especially as the difficulty level increases and the puzzles begin to incorporate more elements (such as increased ambiguity and multiple possibilities for character orientation). Productive failure in mathematics (Kapur 2016), however, is one way to guide instruction. Learners’ failed attempts provide teachers with rich information about their thinking and problem-solving skills that can guide further instruction.
The range of difficulty in the Archelino puzzles also allows for differentiation in the classroom. Additionally, to support all learners in solving the Archelino puzzles, teachers can use different scaffolding tools (such as a number line in front of the ark, labels for the positions on the ark, or left and right directional signs beside the ark).
Collaboration
Pérez (2018, 449) defines collaboration as a “tendency to coordinate effort and negotiate meaning with peers to accomplish a shared goal.”
As a partner or a parent–child activity, playing Archelino allows for working together to complete the given task. At first, students can complete the puzzle by listening to instructions provided by the teacher or a parent. With explicit teaching, students can move to providing oral instructions to their peers.
Completing the puzzle as a whole-class activity, as explored earlier, encourages students to work together. In this setting, deliberate and intentional sequencing of the sharing of important variations in strategies allows students to experience situational ambiguity (Pérez 2018) and make connections as they discuss possible solution pathways. For example, immediate feedback from watching a partner place animals in the ark can lead to discussions about strategy and the specificity of instructions. Overall, this activity allows students to practise collaboration as part of developing computational thinking dispositions.
Archelino allows teachers to focus on developing computational thinking dispositions by explicitly teaching the concepts and by encouraging students to notice, name and nurture the computational thinking in this activity. Pérez’s (2018) framework gives teachers a tool to guide instruction, explore student dispositions and improve how they approach computational thinking tasks in the classroom. Explicitly teaching young students this important construct can help them notice, name and nurture computational thinking opportunities in their later studies.
The framework also gives teachers an important tool for gauging students’ computational thinking dispositions and planning further instruction. Like Pérez, we believe that these dispositions are malleable and that students can work toward improving their computational thinking dispositions over time.
Conclusion
Several good low-floor, unplugged activities for developing the skills and dispositions of computational thinking with young learners, as well as with teachers new to computational thinking, already exist. Commercially available or publicly accessible puzzle games, such as Archelino, allow teachers to bring computational thinking and mathematical ideas into the classroom in a nonthreatening way while developing a healthy disposition.
We have attempted to show readers how a game-based resource can be used to encourage discussion and engagement with foundational computational thinking ideas, such as decomposition and sequencing, together with early mathematical concepts, such as ordering and orientation. It is our hope that after reading this article, readers will be more alert to opportunities to explore foundational computational thinking ideas through resources they already have at hand.
Notes
- This statement and the previous one are excerpts from early written reflections and conversations during team meetings.
- See https://new.learnalberta.ca/Resources/content/cda/documents/math_en.pdf (accessed September 10, 2019).
- See www.iste.org/standards/standards/for-students/(accessed September 10, 2019).
- A downloadable poster is available at https://docs.google.com/drawings/d/1TT4KSdJG_Taas9ksEK8qlc3t59kFPjLDsI7D6ihhNdk/edit (accessed September 10, 2019).
- A downloadable lesson poster is available at https://docs.google.com/drawings/d/12lP87PzgFWwkkfp4oG96cDm5_8bNbOicAeI5FB9MXzg/edit (accessed September 10, 2019).
References
Bers, M U. 2017. Coding as a Playground: Programming and Computational Thinking in the Early Childhood Classroom. New York: Routledge.
Csizmadia, A, P Curzon, M Dorling, S Humphreys, T Ng, C Selby and J Woollard. 2015. Computational Thinking: A Guide for Teachers. Swindon, UK: Computing at School. Also available at http://community.computingatschool.org.uk/files/6695/original.pdf (accessed September 10, 2019).
Denning, P J. 2017. “Remaining Trouble Spots with Computational Thinking.” Communications of the ACM 60, no 6 (June): 33–39.
Freudenthal, H. 1971. “Geometry Between the Devil and the Deep Sea.” Educational Studies in Mathematics 3, nos 3–4 (June): 413–35. Cited in Trninic 2018.
Hoyles, C, and R Noss. 2015. “Revisiting Programming to Enhance Mathematics Learning.” Keynote address at the Math + Coding Symposium, Western University, London, Ont, June 19–21.
Kafai, Y B, and Q Burke. 2014. Connected Code: Why Children Need to Learn Programming. Cambridge, Mass: MIT Press.
Kapur, M. 2016. “Examining Productive Failure, Productive Success, Unproductive Failure, and Unproductive Success in Learning.” Educational Psychologist 51, no 2: 289–99.
Khan, S, I Namukasa, C Yiu, S Rodney and V Guyevskey. 2017. “Report of Working Group on the Integration of Computational Thinking and Mathematics Teaching and Learning in Preschool to Undergraduate and Teacher Education Settings.” Report presented at the Computational Thinking in Mathematics Education Symposium, University of Ontario Institute of Technology, Oshawa, Ont, October 13–15. Also available at http://ctmath.ca/wp-content/uploads/2018/10/Symposium_Working-Group-Report_Khan-Et-al-1.pdf (accessed September 10, 2019).
Kotsopoulos, D, L Floyd, V Nelson and S Makosz. 2019. “Mathematical or Computational Thinking? An Early Years Perspective.” In Mathematical Learning and Cognition in Early Childhood: Integrating Interdisciplinary Research into Practice, ed K M Robinson, H P Osana and D Kotsopoulos, 79–90. Cham, Switzerland: Springer.
Lobato, J, B Rhodehamel and C Hohensee. 2012. “‘Noticing’ as an Alternative Transfer of Learning Process.” Journal of the Learning Sciences 21, no 3: 433–82.
Marton, F. 2014. Necessary Conditions of Learning. New York: Routledge.
Namukasa, I K. 2018. “Enacting Computational Thinking Concepts at Different Levels.” Math + Code ’Zine 3, no 1 (March). http://researchideas.ca/mc/computational-thinking-activities-enacting-concepts-at-different-levels/ (accessed September 10, 2019).
Pérez, A. 2018. “A Framework for Computational Thinking Dispositions in Mathematics Education.” Journal for Research in Mathematics Education 49, no 4 (July): 424–61.
Polya, G. 2014. How to Solve It: A New Aspect of Mathematical Method. Princeton, NJ: Princeton University Press. (Orig pub 1945.)
Resnick, M. 2016. “Designing for Wide Walls.” Design.blog (blog). August 25. https://design.blog/2016/08/25/mitchel-resnick-designing-for-wide-walls/ (accessed September 10, 2019).
Rich, K M, C Strickland, T A Binkowski, C Moran and D Franklin. 2017. “K–8 Learning Trajectories Derived from Research Literature: Sequence, Repetition, Conditionals.” In Proceedings of the 2017 ACM Conference on International Computing Education Research, 182–90. New York: Association for Computing Machinery (ACM).
Salomon, G, and D N Perkins. 1989. “Rocky Roads to Transfer: Rethinking Mechanisms of a Neglected Phenomenon.” Educational Psychologist 24, no 2: 113–42.
Shute, V J, C Sun and J Asbell-Clarke. 2017. “Demystifying Computational Thinking.” Educational Research Review 22 (November): 142–58.
Sung, W, J Ahn and J B Black. 2017. “Introducing Computational Thinking to Young Learners: Practicing Computational Perspectives Through Embodiment in Mathematics Education.” Technology, Knowledge and Learning 22, no 3 (October): 443–63.
Trninic, D. 2018. “Instruction, Repetition, Discovery: Restoring the Historical Educational Role of Practice.” Instructional Science 46, no 1 (February): 133–53. Also available at www.researchgate.net/publication/322078583_Instruction_repetition_discovery_restoring_the_historical_educational_role_of_practice (accessed September 10, 2019).
Whitehead, A N. 1967. “The Aims of Education.” In “The Aims of Education” and Other Essays, 1–14. New York: Free Press. (Orig pub 1929.)
Wing, J M. 2006. “Computational Thinking.” Communications of the ACM 49, no 3 (March): 33–35.
Sally Rudakoff is a teacher and an assistant principal with St Albert Public Schools.
Steven Khan is an assistant professor of mathematics education and computational thinking in the Department of Elementary Education at the University of Alberta.